Deskriptiv
Kvantitative data
Kategoriske data
Intervaller
Analytisk
Sandsynligheder
Kategoriske udfald
Kategoriske eksponeringerLogistisk regression
Kvantitative udfald
Kvantitative udfaldLinær regression
Korrelationer
Overlevelse
Poisson regression
Tilfældighed
Randomisering
Forskning
PhD thesis

Jacob Liljehult
Klinisk sygeplejespecialist
cand.scient.san, Ph.d.
Neurologisk afdeling
Nordsjællands Hospital
Overlevelsesanalyse
Overlevelsesmodeller (eller survival-modeller) er intensitetsbaserede modeller hvor udfaldet måles i hvor lang tid der går indtil et binomialt event.
Datastruktur
Modellerne skal bruge tre variable:
1) En event-variable, der angiver om hændelsen er indtruffet eller ej. Variablen skal være logical
(TRUE/FALSE) når den indgår - men det nemmeste er at kode variablen som enten factor eller integer
med to niveauer, som derefter omformateres i modellen som variable == reference;
2) En tidsvariable, der angiver tiden fra start til enten forekomsten af eventet eller til frafald. Variablen
kan enten være numeric eller interger.
Hvis udfaldet er dødsfald efter inklusion i studiet vil variablen angive tiden indtil at deltageren enten dør eller
frafalder studiet; hvis deltageren dør kodes event-variablen som fx: TRUE (logical), 1 (numical/integer), "Dead" (factor)
og hvis deltageren frafalder som fx: FALSE (logical), 0 (numical/integer), "Alive" (factor). Hvis deltageren overlever indtil
afslutningen af opfølgningen kodes variablen på samme måde som ved frafald, men med tiden for sidste opfølgning;
3) En eksponeringsvariabel som både kan være kvantitativ (numeric/integer) og kategorisk (factor).
Grundformlen for modellen bliver således:
surv(tidsvariabel, event-variabel == reference-værdi) ~ eksponering
Yderligere kan modellen justeres for kovariate ved at tilføje dem på højre side af formlen:
surv(tidsvariabel, event-variabel == reference-værdi) ~ eksponering + kovariate
Eksempel
Som eksempel bruges data fra et kohortestudie med 1031 patienter med apopleksi, der er fulgt i et år efter de blev
indlagt. Udfaldet er tid indtil dødsfald og som eksempel bruges en variabel med to subtyper IS (ischemic stroke) og
ICH (intracerebral heamorrhage):
strokedata <- read.csv(" https://jacobliljehult.github.io/research/strokedata.csv", sep=",", header=T, stringsAsFactors = TRUE)
library(dplyr)
rbind(
strokedata %>%
select(daystomors, mors1y, diagnosis) %>%
arrange(daystomors) %>%
filter(row_number() <= 5, row_number() >= 1),
strokedata %>%
select(daystomors, mors1y, diagnosis) %>%
arrange(-daystomors) %>%
filter(row_number() <= 5, row_number() >= 1))
| daystomors | mors1y | diagnosis | |
|---|---|---|---|
| 1 | 0 | Dead | ICH |
| 2 | 0 | Alive | ICH |
| 3 | 0 | Dead | ICH |
| 4 | 0 | Dead | ICH |
| 5 | 0 | Dead | IS |
| 6 | 1597 | Alive | IS |
| 7 | 1595 | Alive | IS |
| 8 | 1595 | Alive | IS |
| 9 | 1595 | Alive | IS |
| 10 | 1595 | Alive | IS |
De tre variable indeholder følgende information:
daysomors - antallet af dage til dødsfald (eller frafald) indtil 1595 dage efter indlæggelsestidspunktet;
mors1y - dichotom factor-variabel der angiver om patienten er død eller levende et år efter indlæggelsesdagen; og
diagnosis - factor-variabel der angiver subtypen dichotomt som enten IS eller ICH
Cox' Proportional Hazard regression
Proportional hazard regression kan laves med funktionen coxph() fra pakken {survival} med syntaksen:
coxph( Surv( t, e == r) ~ x, data = df).
Resultatet af modellen vises med funktionen summary().
library(survival)
model1 <- coxph(Surv(daystomors, mors1y == "Dead") ~ diagnosis,
data = strokedata)
summary(model1)
coxph(formula = Surv(daystomors, mors1y == "Dead") ~ diagnosis, data = strokedata)
n = 1031, number of events= 186
| coef | exp(coef) | se(coef) | z | Pr(>|z|) | ||
|---|---|---|---|---|---|---|
| diagnosisIS | -1.0522 | 0.3492 | 0.1770 | -5.945 | 2.76e-09 | *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
| exp(coef) | exp(-coef) | lower .95 | upper .95 | |
|---|---|---|---|---|
| diagnosisIS | 0.3492 | 2.864 | 0.2468 | 0.494 |
Concordance = 0.567 (se = 0.015 )
| Likelihood ratio test | = 28.65 | on 1 df, | p=9e-08 |
|---|---|---|---|
| Wald test | = 35.35 | on 1 df, | p=3e-09 |
| Score (logrank) test | = 38.73 | on 1 df, | p=5e-10 |
Outputtet fra summary() funktionen indeholder både koefficienten på eksponentiel skala
(coef) og hazard ratio (exp(coef)), samt konfidensintervallet for hazard ratioen,
men kan være lidt svær at overskue. Et lidt mere overskueligt output kan man få med publish() funktionen
fra pakken {Publish}:
Publish::publish(model1)
| Variable | Units | HazardRatio | CI.95 | p-value |
|---|---|---|---|---|
| diagnosis | ICH | Ref | ||
| IS | 0.35 | [0.25;0.49] | <0.001 |
Referenceværdien for eksponeringsvariablen kan ændres med funktionen relevel():
model2 <- coxph(Surv(daystomors, mors1y == "Dead") ~
relevel(diagnosis, ref="IS"), data = strokedata)
Publish::publish(model2)
| Variable | Units | HazardRatio | CI.95 | p-value |
|---|---|---|---|---|
| relevel(diagnosis, ref = "IS") | IS | Ref | ||
| ICH | 2.86 | [2.02;4.05] | <0.001 |
Modellen kan justeres for en kovariate ved at forbinde dem med x-variablen på højre side af formlen:
model3 <- coxph(Surv(daystomors, mors1y == "Dead") ~
relevel(diagnosis, ref="IS") + age, data = strokedata)
Publish::publish(model3)
| Variable | Units | HazardRatio | CI.95 | p-value |
|---|---|---|---|---|
| relevel(diagnosis, ref = "IS") | IS | Ref | ||
| ICH | 2.83 | [2.00;4.01] | <0.001 | |
| age | 1.10 | [1.08;1.12] | <0.001 |
Goodness-of-fit
Log-liklihood ratio test kan bruges til at sammenligne to nestede Cox modeller, hvis man ønsker en formel test af om tilføjelsen af en kovariat bidrager med yderligere information til modellen.
Dette kan enten gøres med funktionen lrtest() fra pakken {lmtest}:
Model 1: Surv(daystomors, mors1y == "Dead") ~ relevel(diagnosis, ref = "IS")
Model 2: Surv(daystomors, mors1y == "Dead") ~ relevel(diagnosis, ref = "IS") + age
| #Df | LogLik | Df | Chisq | Pr(>Chisq) | ||
|---|---|---|---|---|---|---|
| 1 | 1 | -1257.4 | ||||
| 2 | 2 | -1173.7 | 1 | 167.44 | < 2.2e-16 | *** |
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
eller manuelt:
b <- unname( summary(model3)$logtest[1] )
c <- (a-b)
a
b
c
pchisq(abs(c), df= 1, lower.tail = FALSE)
[1] 196.0886
[1] -167.4364
[1] 2.68599e-38
Her hentes først log-test estimaterne fra de to modeller med summary(x)$logtest[1].
Funktionen unname(), der er sat omkring, bruges kun til at fjerne tekst-attributen
"test" fra outputtet så der kun returneres tallet - hvilket mest er af æstetiske grunde.
Forskellen mellem log-test estimaterne følger en chi2-fordeling og p-værdien kan derfor udregnes med
funktionen pchisq(x , df = df, lower.tail = FALSE).
Funktionen
abs(x) bruges til at fjerne fortegnet fra inputtet, så det er ligegyldigt hvordan man
trækker log-test estimaterne fra hinanden (chi2-værdien kan kun være positiv)
Log-rank test
Log-rank test kan laves med funktionen survdiff() fra pakken {survival}:
library(survival)
survdiff(Surv(daystomors, mors1y == "Dead") ~ relevel(diagnosis, ref="IS"),
data = strokedata)
survdiff(formula = Surv(daystomors, mors1y == "Dead") ~
relevel(diagnosis, ref = "IS"), data = strokedata)
| N | Observed | Expected | (O-E)^2/E | (O-E)^2/V | |
|---|---|---|---|---|---|
| relevel(diagnosis, ref = "IS")=IS | 921 | 145 | 169.2 | 3.47 | 38.6 |
| relevel(diagnosis, ref = "IS")=ICH | 110 | 41 | 16.8 | 35.06 | 38.6 |
Chisq= 38.6 on 1 degrees of freedom, p= 5e-10
Kaplan-Meier plot
Overlevelsesanalyser kan illustreres ved hjælp af Kaplan-Meier plots med funktionen survfit
fra pakken {survminer}
Kaplan-meier plot for ovenstående modeller:
library(survminer)
fit1 <- survfit(
Surv(daystomors, mors1y == "Dead") ~ relevel(diagnosis, ref="IS"),
data = strokedata)
ggsurvplot(fit1)
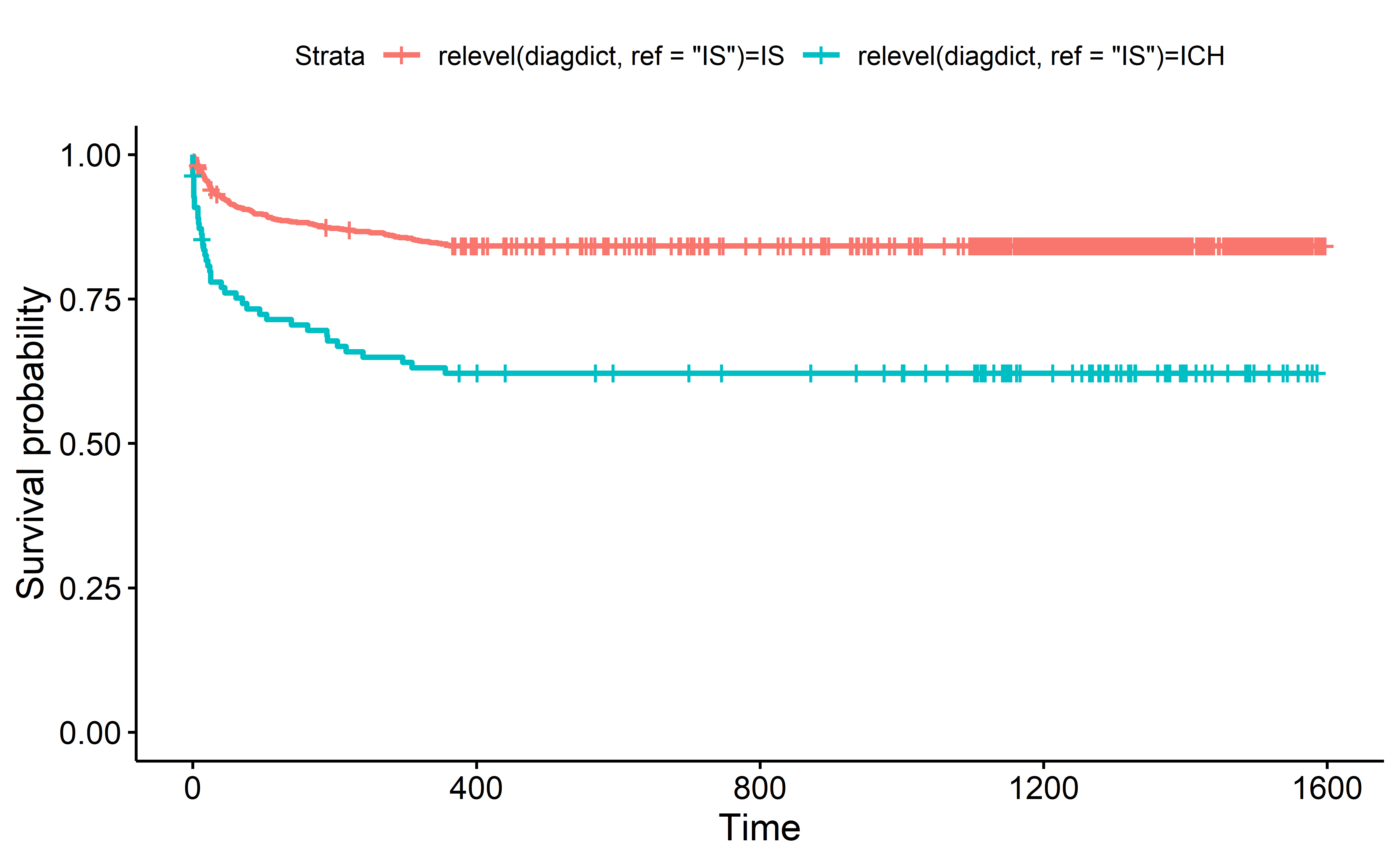
Problemet med dette plot er at tids- og eventvariablene har forskellige tidsperspektiver: Event-variablen angiver kun dødsfald indenfor det første år, men tidsvariablen angiver tid indtil dødsfald op til fire år efter; med det resultat at alle dødsfald efter 366 dage bortcensoreres. Man kan derfor tilføje argumenter for at styre hvordan plottet skal renderes:
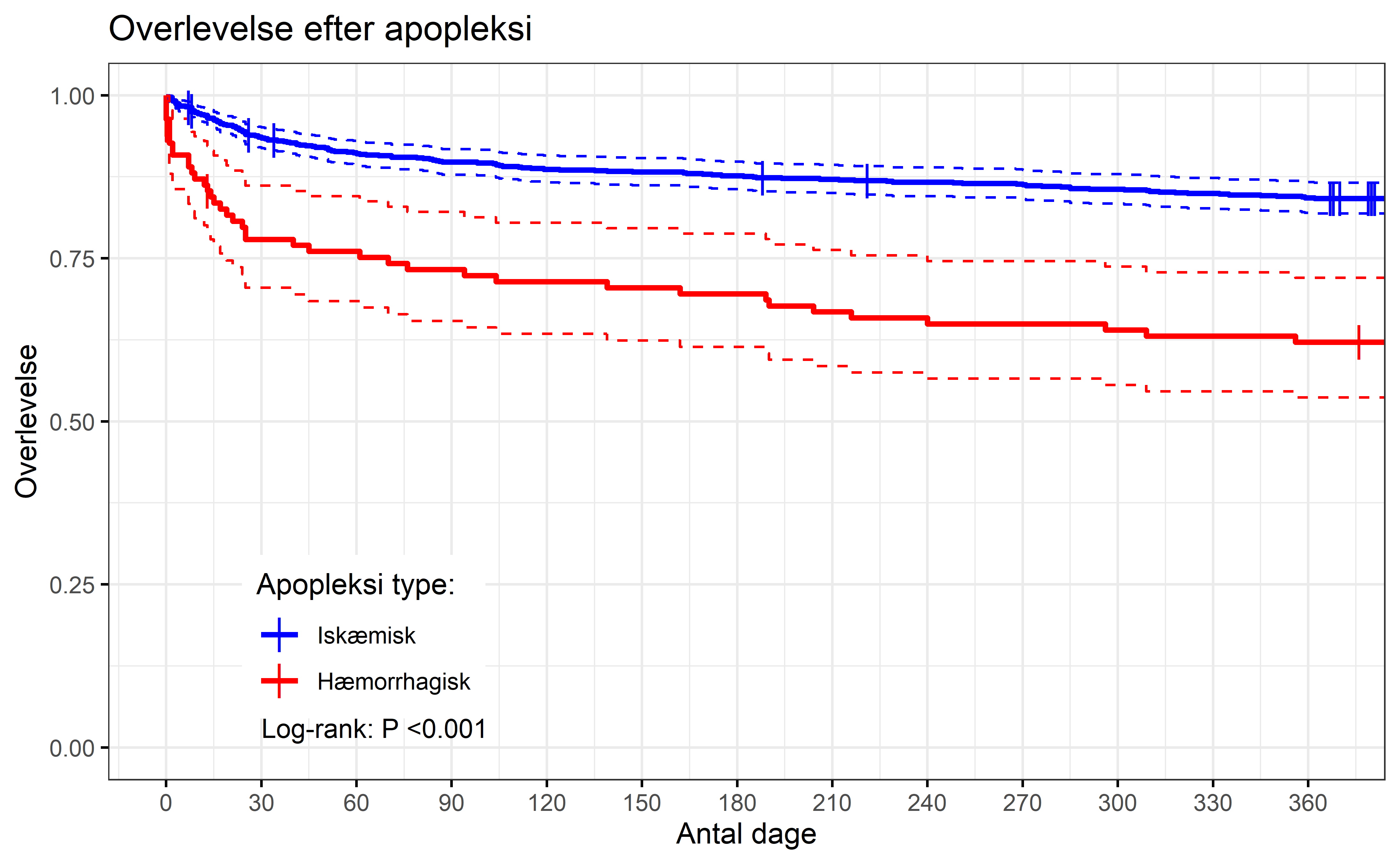
ggsurvplot(fit1,
xlim = c(0,366), # Afgrænser x-aksen til 366 dage
break.time.by = 30, # Opdeler x-aksen i 30 dages intervaller
conf.int = TRUE, # Tilføjer konfidensintervaller
conf.int.style = "step",
palette = c("blue","red"), # Farven på kurverne
ggtheme = theme_bw(), # Figurtemaet
pval = "Log-rank: P <0.001", pval.coord = c(30,0.03), pval.size = 3.5,
censor.shape= "|", # Angivelse af censur på kurven
title = "Overlevelse efter apopleksi",
ylab = "Overlevelse", xlab = "Antal dage",
legend = c(0.2, 0.2), # Placeringen af forklaringen inde i figuren
legend.title = "Apopleksi type:", # Titel på forklaringen
legend.labs = c("Iskæmisk", "Hæmorrhagisk"), # Labels på forklaringen
)