Deskriptiv
Kvantitative data
Kategoriske data
Intervaller
Analytisk
Sandsynligheder
Kategoriske udfald
Kategoriske eksponeringerLogistisk regression
Kvantitative udfald
Kvantitative udfaldLinær regression
Korrelationer
Overlevelse
Poisson regression
Tilfældighed
Randomisering
Forskning
PhD thesis

Jacob Liljehult
Klinisk sygeplejespecialist
cand.scient.san, Ph.d.
Neurologisk afdeling
Nordsjællands Hospital
Korrelation
korrelations analyser laves alle med funktionen cor.test( x, y, method) hvor argumentet method bruges til at styre hvilken analyse der laves ved at definere den som enten "pearson", "kendall" eller "spearman".
Parametrisk test
Pearson's r-test
with(strokedata, cor.test(SBT, DBT, method = 'pearson'))
Pearson's product-moment correlation
data: SBT and DBT
t = 19.663, df = 1029, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.4767690 0.5656165
sample estimates:
cor
0.5226102
Modelantagelser
Pearson's r test antager at begge variable er normalfordelte - og ikke bare at residualerne er normaltfordelte som ved linær regression.
Den letteste måde at undersøge om denne antagelse er opfyldt er ved at visualisere data. Det kan gøres helt simpelt med funktionen plot( x, y) der findes i base R, mens pakken {ggplot2} giver mere fleksibilitet i forhold til at lægge flere lag på plottet (fx smooth linjer).
ggplot(aes(x = SBT, y = DBT), data = strokedata) +
geom_point(alpha = 0.5, color = "black") +
geom_smooth() + # Indsætter smoothlinje (blå)
geom_smooth(method = lm, se = FALSE, color = "red", linetype = 2) + # Indsætter linær smoothlinje (rød)
theme_classic()
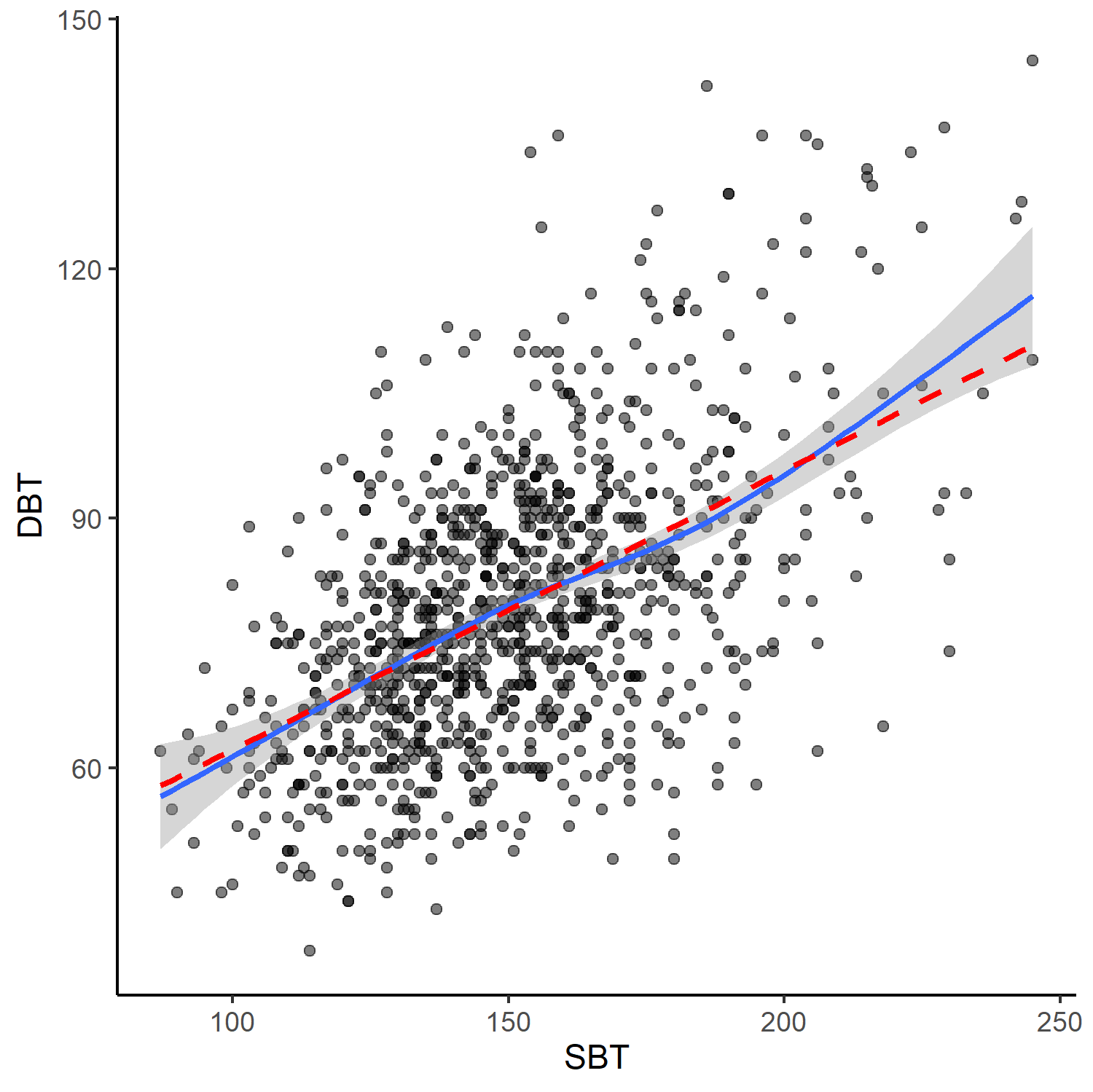
Systolisk blodtryk plottet imod diastolisk blodtryk. Blå linje: Loess kurve med konfidensinterval. Rød/stiplet linje: Linær tendens
For at gøre det endnu tydeligere:
library(ggpubr)
library(patchwork)
pointplot <- ggplot(aes(x = SBT, y = DBT), data = strokedata) +
stat_density_2d(aes(fill = ..level..), geom = "polygon", alpha = 0.5) +
scale_fill_gradient(low = "yellow", high = "brown") +
geom_density_2d(aes(fill = ..level..), geom = "polygon", alpha = 0.5,
color="black", linetype = 2) +
geom_point(alpha = 0.5, color = "black") + geom_smooth() +
geom_smooth(method = lm, se = FALSE, color = "red", linetype = 2) +
theme_classic() +
theme(legend.position = "none")
dens1 <- ggplot(strokedata, aes(x = SBT)) +
geom_histogram(alpha = 0.4, color = "black") +
theme_void() +
theme(legend.position = "none")
dens2 <- ggplot(strokedata, aes(x = DBT)) +
geom_histogram(alpha = 0.4, color = "black") +
theme_void() +
theme(legend.position = "none") + coord_flip()
dens1 + plot_spacer() + pointplot + dens2 +
plot_layout(ncol = 2, nrow = 2, widths = c(4, 1), heights = c(1, 4))
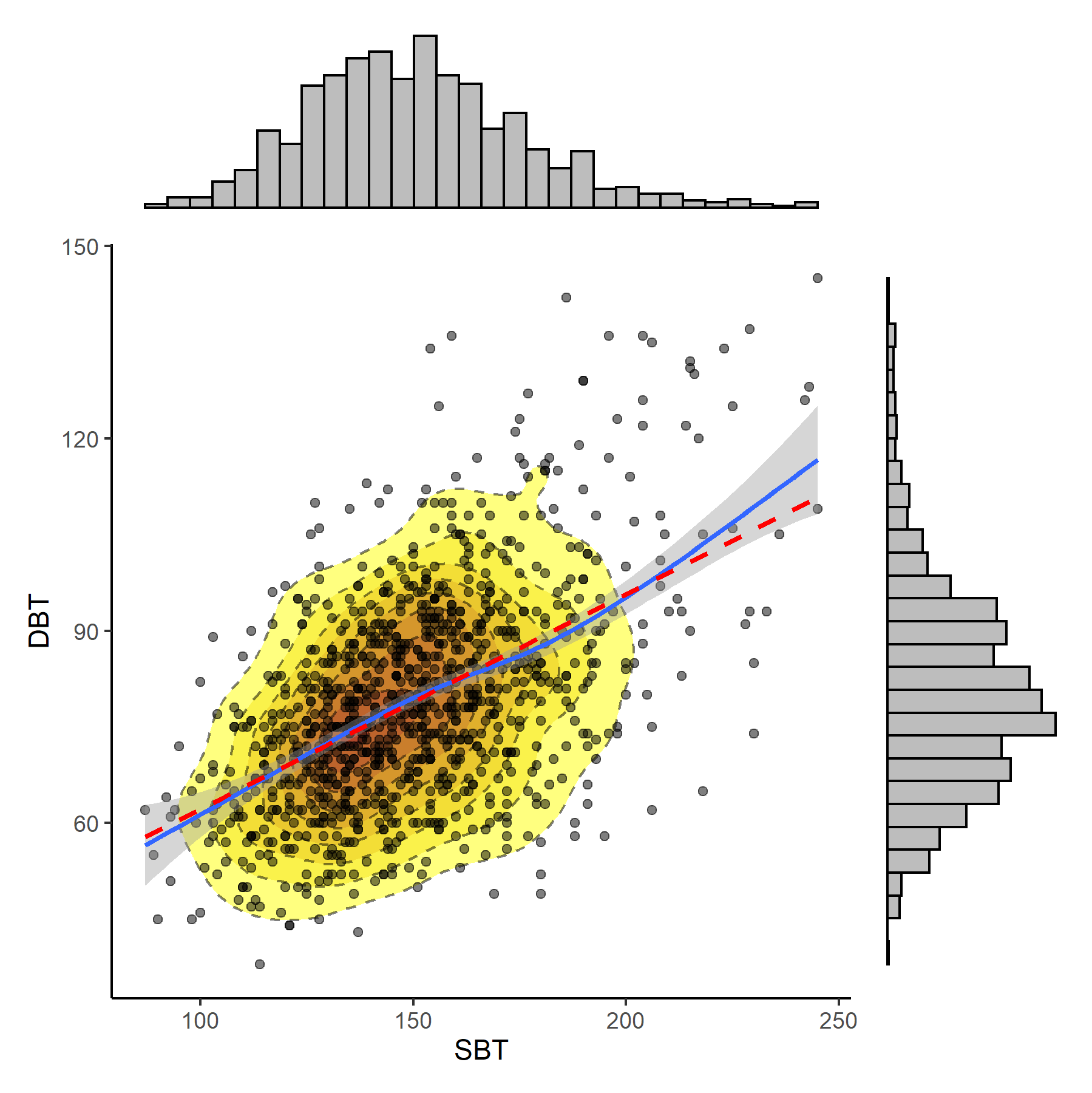
Systolisk blodtryk plottet imod diastolisk blodtryk. På siderne er der tilføjet histogrammer for hver variabel og under punkterne er der tilføjet et to-dimensionelt density område (jo tættere punkter, des mørkere område)
Blå linje: Loess kurve med konfidensinterval. Rød/stiplet linje: Linær tendens
Non-parametriske tests
Hvis man skal lave korrelationsanalyser på data der ikke opfylder modelantagelserne for Pearson's r-test, kan man i stedet bruge en non-parametrisk test. Ulempen er at tau og rho ikke kan fortolkes så direkte som r, men man får under alle omstændigheder en p-værdi.
Som eksempel kan vi undersøge korrelationen mellem symptombyrden hos patienter med apopleksi (sss) og abnorme vitalparametre (EWS):
geom_point(alpha = 0.5, color = "black") +
geom_smooth() +
geom_smooth(method = lm, se = FALSE, color = "red", linetype = 2) +
theme_classic()
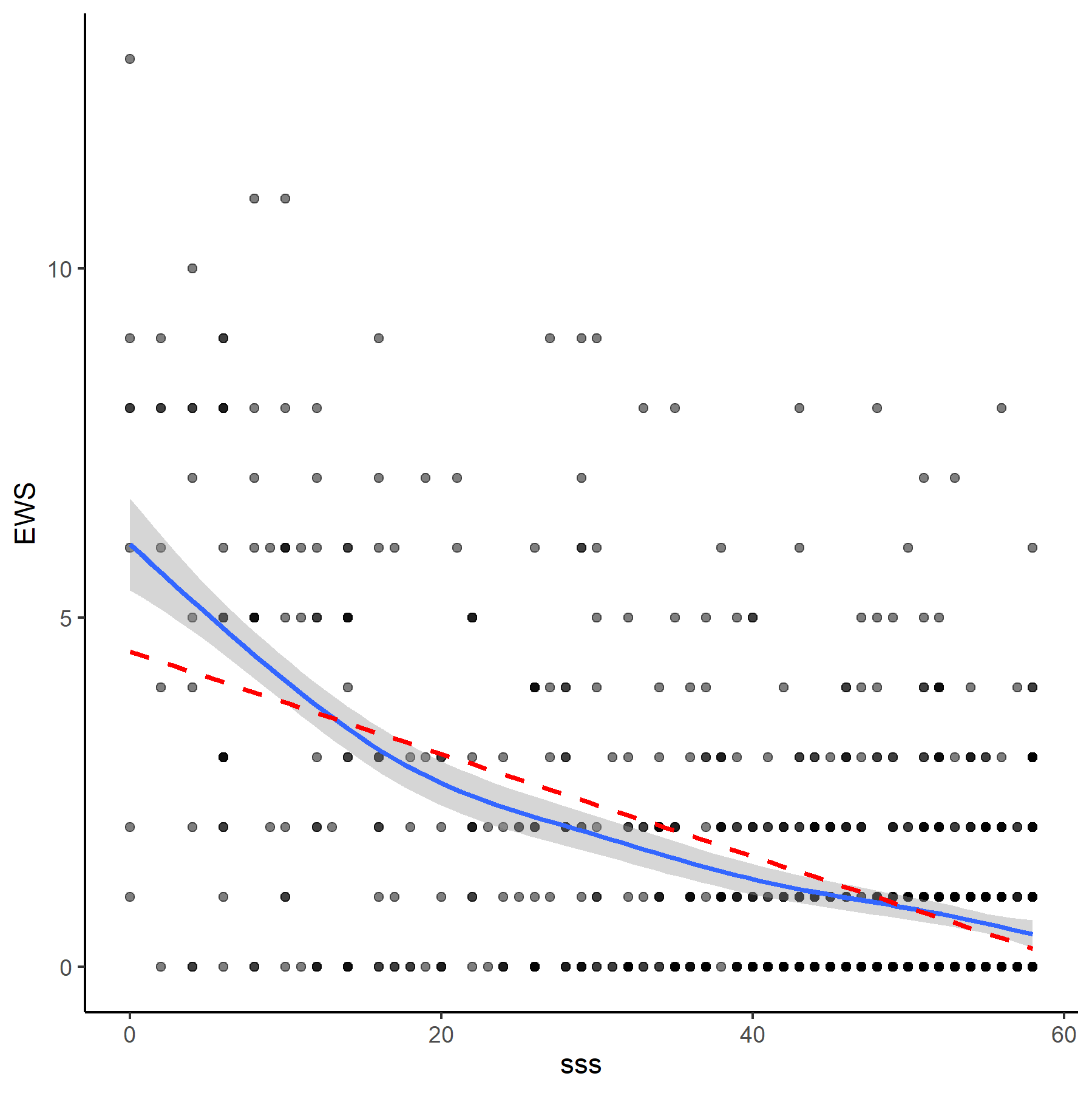
Scandinavian Stroke Scale plottet imod Early Warning Score. Blå linje: Loess kurve med konfidensinterval. Rød/stiplet linje: Linær tendens
Kendall's tau
with(strokedata, cor.test(sss, EWS, method = 'kendall' ))
Kendall's rank correlation tau
data: sss and EWS
z = -13.724, p-value < 2.2e-16
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
-0.3277317
Spearman's rho
with(strokedata, cor.test(sss, EWS, method = 'spearman' ))
Spearman's rank correlation rho
data: sss and EWS
S = 258010049, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.4125775